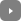Power satellites are an idea that has been around since the late 1960s but not developed commercially because we don't know how to build an inexpensive space transport system. That may have changed recently, at least in theory.
We have known for decades that solar power satellites can send energy to the earth. Communication satellites do it every day, just not at levels useful for power. Power satellites scale to humanity's need; a calculation by G. Harry Stein back in the 1980s noted that there was room for 177 TW in geosynchronous orbit (more than ten times current energy use).
The concept is to make electric power in space (thermal or photovoltaic), turn the power into microwaves, beam the microwaves to Earth and convert them back to electric power at "rectennas." The rectennas are simple (though large) structures that stop so little sunlight that the intention is to place them over farmland within a few hundred km of cities.
The biggest obstacle to solar power satellites is the cost of putting the necessary hardware in space. What this current post does is describe a way to reduce the cost of putting the materials into space far enough that energy from power satellites can compete with coal (2 cents per kWh), assuming we amortize the total cost over a 10-year period.
Introduction
Power satellites convert sunlight (via photovoltaic or thermal cycle) to electrical power and then turn the power into microwaves beamed to the ground and converted back to electrical power.
Power satellites are a way of harvesting dilute solar energy with several advantages over the solar PV on the ground or rooftops:
• A system of power satellites scales to human civilization's needs (tens of TW).
• They don't need storage since their location (the 24 hour orbit, geosynchronous or GEO) is illuminated 99% of the time. (Satellite TV antennas point to a location on that orbit.)
• No day-night cycle and no clouds or air gives power satellites an average advantage of about nine times over the same area of solar collectors on the ground.
• Power satellites use relatively little material. Being in orbit (zero gravity), and no wind they can be much lighter per kW than collecting sunlight on the ground.
• They have a very short energy payback time.
They have some disadvantages, however:
• For optical reasons, they don't scale down to small sizes; 5 GW is about as small as you want to make one.
• At 50% loss electricity-in space to electricity-on-the-ground, the cost is doubled from one cent per kWh to two. On the other hand, that's 40 times less cost than transmitting the same power over wires for the same distance.
• They take a large investment to get the cost of transporting parts to GEO down to where they make economic sense.
Cost Requirements to make Space Solar Power Economical
Is a space solar project worth doing? We need to run a cost/benefit analysis to find out.
For a ten-year return on capital, a kW of power sold for a penny a kWh generates $800 of revenue (~80,000 revenue-hours in ten years). Two cents per kWh is about the most power could sell for to displace coal. That means a kW of power satellite capacity can't cost more than $1600 or $1.6 B per GW if it is to meet this goal.
If power satellites take 5 kg of parts to generate a kW on the ground, and the transport fraction is ~1/3, then the cost to lift parts to GEO can be no more than $100/kg. That's a reduction of 200 to one ($20,000 per kg down to $100) over current cost to deliver communication satellites to GEO.
Hiroshi Yoshida, Chief Executive Officer of Excalibur KK, a Tokyo-based space and defense-policy consulting company, and William Maness, chief executive officer of Everett, Wash.-based PowerSat Corp., both think it will take this kind of transport cost reduction for power satellites to be competitive with other power sources.
Conventional Rockets
Can we get to this lift cost with conventional rockets?
Unfortunately, the answer is no, for several reasons. The chemical energy in rocket fuel vs. the required energy it takes to get to orbit is not enough. Rocket technology with chemical fuels has reached the performance limit. The most promising design is the Falcon Heavy (a proposal of SpaceX), with first launch intended for 2012 at a cost of $100 M per trip. The rocket is expected to put 53 tons in low earth orbit (190 km) above the earth’s surface, or 19.5 tons in geostationary orbit at 36,000 km. That is a reduction to $4000/kg, a factor of five below current rockets, but not enough. Launching a Falcon Heavy every hour might get the price down to $1000/kg, which is still too high by a factor of ten.
Reaction Engine has a developed a rocket plane called Skylon that is intended to be an improvement over conventional rockets.

Figure 1 – Reaction Engine’s proposed rocket plane (source)
Reaction Engine's study of Skylon indicates it will put 12 tons in LEO or (with a second stage) 5 tons in GEO for an estimated cost of $1.5 M or $300/kg. The project goal is to develop an unpiloted space plane that can be re-used up to 200-500 times. The expected cost per kg depends on the flight rate per year:

Figure 2 – Skylon specific launch price as a function of flight rate (Source: Figure 10 from Solar Power Satellites and Spaceplanes)
Unfortunately the cost is still too high by a factor of three. And it takes a flight rate of several per hour to get the cost that low. Are we out of luck and solar energy will stream past the earth forever? Not necessarily.
Skylon Sub Orbital plus Laser Propulsion
The new concept presented here is to use the Skylon sub orbital maximum load of 30 tons for a second stage (see Appendix: Into Orbit—Sideways below, also Wikipedia-Multistage Rocket). The second stage propulsion would be hydrogen heated to 3000 deg K by a (relatively small) 500 MW array of ground-based lasers.

Figure 3 – Diagram by Jordin Kare HX Laser Launch: It’s Steamship Time
The system with ground-based lasers would function as follows:
• The laser beams go up to an array of tracking mirrors in geosynchronous orbit over a point 3500 km to the east of where the second stage release point.
• The ground lasers point at the bounce mirrors which track the accelerating laser powered second stage over 11 degrees. (The mirrors move 5.5 degrees in 16 minutes.)
• Hydrogen at 3000 deg K gives the second stage ~10km/s exhaust velocity. This velocity is about twice the required delta V for a mass ratio of ~1.65.
In this system,18-20 tons of 30 will arrive at GEO per flight. The capital cost for the lasers ($5 B or $500 M/year) is about $1/kg when spread over 480,000 tons of cargo per year and it drives the lift cost for parts down to $100/kg. In maximum payload sub orbital mode, Skylon is projected to boost a 30-ton payload to 157 km apogee and 6966 m/s. See page 10 from this manual.
To avoid excessive aerodynamic heating, the payload release is delayed to 135 km. Unpowered, the payload would take 150 seconds to reach apogee. A velocity of 6966 m/s is ~1000 m/s short of LEO and 3286 m/s short of geosynchronous transfer orbit (GTO).
An acceleration of more than two m/s2has enough time to put the second stage into orbit. The second stage loses upward velocity slowly because the effective g at 87% of orbital speed is low, around two m/s2. Under light acceleration (see below graph), the second stage gets to orbital velocity before it runs out of upward motion.

Figure 4 – Graph generated by author of Path to Geosynchronous Transfer Orbit
There are limits on how long and how slow the second stage can be accelerated with a laser. The vehicle has to stay in view of the bounce mirror in GEO and it has to exceed orbital speed before it falls back into the atmosphere.
The normal metric for laser launch from the ground is around a GW per ton of payload. If you need a cargo size of 20 tons (about the minimum for power satellites) that means 20 GW of laser, drawing 40 GW off the grid and costing perhaps $200 B. This is partly because the very high exhaust velocity of laser propulsion is energy inefficient until the vehicle is up to a velocity comparable to the exhaust velocity and partly due to the short time the vehicle is in view of a ground laser. The following are some ways the cost might possibly be reduced:
• Bounce mirrors, for all the complications of being in GEO and having to track the vehicle, reduce the amount of laser power needed for 20-ton payload to GEO by a factor of 50. They do this by allowing an acceleration of less than one g and by permitting the laser to be on target for roughly 4 times as long as is practical for a ground up launch. (See Figure 5 below.)
• It does require a chemical rocket or rocket plane boost to near orbital velocity but from 50% to 150% their exhaust velocity is where chemical rockets work most efficiently. (See http://en.wikipedia.org/wiki/File:PropulsiveEfficiency.svg.) Up to the end of using air at 26 km and two km/sec (44% of Skylon's rocket mode exhaust velocity) aerospace planes in air breathing mode are very efficient.
• Geosynchronous transfer orbit velocity is 10252 m/s. Circularizing the orbit at GEO requires an additional 1630 m/s for a total delta V from the ground of 11,682 m/s. The exhaust velocity for hydrogen is roughly 9800 * sqrt (T/3000) where T is degrees K
• Together, the extra delta V is 4916 m/s for the second stage--which is about half the exhaust velocity leading to a mass ratio of ~1.65 for the mission or 10-12 tons of reaction mass for 18-20 tons of payload and vehicle. Expending most of the reaction mass low in the earth's gravitational field leads to slightly better performance.
• In various designs, I have used both constant acceleration and constant heater temperature. Constant heater temperature provides higher exhaust velocity and better exhaust velocity performance if it provides enough acceleration to get the vehicle into orbit before it falls into the atmosphere or goes out of view.
• Together the accelerations to GTO and the circularization burn at GTO can't take more than 20 minutes to get a transfer rate of three flights per hour. 10,000 kg of hydrogen over 1200 seconds is 8.33 kg/sec
• The laser power required comes from 8.33 kg/s accelerated to 9.8 km/s. Ke/s = 1/2 mV^2/s, where m is 8.333 kg/sec and V is 9.8 km/ sec--solving, 400 MW.
• There will be some atmospheric and optical loss for the laser beam and some re radiation loss from the vehicle. These should be relatively small (under 20%), raising the laser output to 500 MW and the input (at 50% efficient) to 1 GW.
• The flow of 8.33 kg/s of hydrogen and 400 MW (after loses) results in a constant heater temperature of 3000 deg K (for an exhaust velocity of 9.8 km/s) and an initial acceleration of 2.72 m/s2.
This is an unusual regime for rockets. It is between the low exhaust velocity/high thrust of first stage rockets and the low thrust and very high exhaust velocity of ion drives.
Under these conditions, a second by second spreadsheet analysis shows that a 30 ton second stage vehicle enters GTO downrange 7743 km at 970 seconds with 21,900 kg of mass remaining. Because thrust is constant as mass is used up, the acceleration climbs to 3.727 m/s2 (under 0.4 g). It takes until 1206 seconds to reach the velocity required for GEO insertion, i.e., a second burn 5 or 15 hours later of 236 seconds. For a first pass analysis, this is close enough to 20 minutes.

Figure 5 – Diagram by author.
The peak acceleration at the end of circularizing at GEO is just over four m/s2 (all really low accelerations). According to the spreadsheet, there is almost 20,000 kg (19937 kg) left. I.e., ~20 tons gets to GEO per Skylon flight. We are assuming that everything going to GEO becomes power satellites (even the sandwich wrappers for 500 workers at GEO).
Cost Reduction Details
Conventional use of Skylon will deliver about 5 tons per flight to GEO. For a three per hour flight rate, that's 15 tons per hour. By adding $5 B of lasers (and the GEO bounce mirrors), laser boosting a sub orbital payload will put 60 tons per hr in GEO, that is, 4 times as much. In calculating the economics the following assumptions are made:
• Operating this transport system 90% of the time, it lifts 8000 h/yr x 60 t/h or 480,000 t per year. (That would support a substantial power satellite production.)
• At 5000 t/GW, it would make 96 GW per year (19 five GW power satellites).
• At a price of $1.6 B/GW (2 cents per kWh paid off over ten years), the revenue stream from selling power satellites would be over $150 B per year.
To put the addition of laser powered second stages in context, the same flight rate would allow four times as much cargo to GEO for the same cost in Skylon launches. The capital cost for the lasers ($500 M/year expensed at 10%/year) is about $1/kg when spread over 480,000 tons of cargo per year and it drives the lift cost for parts down to under $100/kg. The cost to GEO (not LEO) would come down to under $100/kg, which is the magic number for two cent per kWh power, i.e., half the price of coal (or less).
Power Satellite Energy Economics
While Energy returned on energy invested (EROEI) is good metric for sources such as oil, coal, and natural gas, which have reserves that are eventually exhausted, the Wikipedia article for Net Energy Gain (NEG) indicates that NEG or payback period might be a better metric for sustainables. According to the article:
The situation is different with sustainable energy sources, such as hydroelectric, wind, solar, and geothermal energy sources, because there is no bulk reserve to account for (other than the Sun's lifetime), but the energy continuously trickles, so only the energy required for extraction is considered.
In all energy extraction cases, the life cycle of the energy-extraction device is crucial for the NEG-ratio. If an extraction device is defunct after 10 years, its NEG will be significantly lower than if it operates for 30 years. Therefore, the energy payback time (sometimes referred to as energy amortization) can be used instead, which is the time, usually given in years, a plant must operate until the running NEG becomes positive (i.e. until the amount of energy needed for the plant infrastructure has been harvested from the plant).
For photovoltaic cells, the NEG of their production depends on the operating lifetime, and the amount of sunlight available in the operating location. Today the break-even energy payback time (the amount of time required to produce an amount of energy equal to that originally used to manufacture the array) is around two to four years, compared to an effective production life of over 20 to 30 years (e.g. many manufacturers now provide a 25-year warranty on their products).
Note the in the last paragraph quoted above indicates that the energy payback period for solar cells is two to four years. The corresponding payback period for wind is given by Renewable UK:
The average wind farm in the UK will pay back the energy used in its manufacture within six to eight months.
The payback time for wind farms doesn't include the backup gas turbines for when there is no wind, nor the energy required for long distance transmission lines to distribute the wind energy to cities far from the production source.
So how do solar power satellites stack up?
Aluminum is the most expensive construction material in terms of releasing it from the oxide and it's less (13 kWh/kg) than the least possible energy investment to get it to GEO (15 kWh/kg). Since the projected transport energy cost are many times more than the energy in aluminum, we can usually ignore of the energy investment in parts for power satellites to make a rough calculation of energy payback time.
A hypothetical moving loop space elevator would require the minimum energy needed to get payload to GEO. For a power satellite made with parts brought up by a minimum energy space elevator, 5 kg (enough for a kW) will take 75 kWh to lift it to GEO. The energy payback time is just over 3 days (6 days if you count the ~75 kWh needed to make aluminum.)
Alas! We don't have and may never get space elevators. What about other ways to get parts to GEO?
• Chemical rockets are around 2.5% energy efficient so the payback time is 40 times that long or about 120 days. That doesn't include the relatively large amounts of energy needed to make the rocket structure, though.
• For the highly reusable Skylon and laser proposal, the laser part, draws around a GW to send 60 t/h to GEO(starting from a sub orbital boost by the Skylon). It also uses 30 ton per hour of hydrogen with an energy content of 210,000 kWh. One million, two hundred and ten kWh/60,000kg is 21 kWh/kg.
• The Skylon boost phase burns 66807 kg of hydrogen per launch; the energy in the hydrogen (at 70 kWh/kg) for three per hour would be 14,029,470 kWh, / 60,000 kg or 233 kWh/kg.
• Together, 254 kWh/kg, (6% efficient compared to the minimum energy) so material for a kW of power satellite would take 1270 kWh to lift--which gives an energy payback time of around 53 days, under two months.
This is substantially shorter payback time than ground solar or wind.
So at least from the physics of rocket planes, laser propulsion, and the energy economics of power satellites, it seems to be possible to have a world with plenty of low cost energy.
This is by no means a fully worked out proposal. For example, how do we get sub orbital Skylons back to their runway? Can we really heat hydrogen with a laser to 3000 deg K? That is 600 deg below melting tungsten but questionable. Carbon is a solid up to 3900 deg K, but at that temperature will it become hydrocarbons?
More analysis might find the entire project to profitability as low as $40 B (half for Skylon development). If that's the case, it's close to the Chunnel or Three Gorges Dam in current dollars.
Appendix: Into Orbit—Sideways
Here's a very rough design of a laser powered second stage to GEO to go with the C1 Skylon.
• The Skylon payload bay is 4.8 across x 13 meters or 62.4 m2. For 400 MW, that is 6.4 MW/m2or 640 W/cm2. That is a lot of heat to be absorbed in a small area, but less than 3 times that of a commercial heat gun per square cm.
• Because we want the laser absorber accurately pointed at the laser beam coming down from geosynchronous orbit the idea would be to put nozzles on each end of a drum shaped vehicle--which would fly sideways into orbit. It would feed 3000 deg K hot hydrogen through a plus or minus 6-degree rotating joint to keep the absorber pointed at the laser beam. Such joints exist on solid rockets.
• The volume of the payload bay is ~ 15 m2 x 13 m or 195 cubic meters. The second stage hydrogen tank (10,000 kg) would occupy 143 cubic meters, leaving 52 cubic meters for 20 tons of heat absorber, tanks, rocket nozzles, pumps and cargo.
The 8.3 kg/s flow of hydrogen needs to be at 5-10 bar. Jordin Kare's micro channel heater design is one approach. Another that would reduce re radiation would be to use a curved piece of transparent aluminum oxide with a cavity light absorber under it (co-flow per http://www.freepatentsonline.com/4033118.pdf). Cold, flowing hydrogen would carry away any energy deposited in the window material.
Ten bar of pressure is a million Pascal. The hoop stress for 4.8 m diameter is 2.4 M N per meter. Tensile for fused aluminum oxide is around 360 M Pa, used at 240 M Pa, it would be one cm thick. The window mass would be around 5 x 13 x .01 x 4000 kg per cubic meter or 2600 kg (or 1300 kg for five bar).
This is OK since everything that gets to GEO becomes parts for power satellites. If you can't use it for anything else, grind it to dust and use it for heat sink pseudo fluid (low pressure gas and fine solids blown around in giant rubberized fabric tubes).
The laser heat absorbers would be useful parts in thermal type power satellites, perhaps down rated to 100 MW. With some thought to the design, much of the second stage pumps and other parts may be useful for constructing power satellites.
By. Keith Henson
This is a guest post by Keith Henson. Keith can be reached at hkeithhenson at gmail dot com.
Source: The Oil Drum