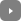A lot of attention has been given to the optimistic assessments of future U.S. and Iraqi oil production in the IEA's World Energy Outlook 2012. However, perhaps even more dramatic is the report's prediction of a significant long-term decline in petroleum consumption from the OECD countries. For example, the report predicts about a 1 mb/d drop in U.S. oil consumption by 2020 and a 5 mb/d drop by 2035 relative to current levels. I was curious to examine some of the fundamentals behind petroleum consumption to assess the plausibility of the IEA projections.

U.S. oil consumption, 12-month averages, Jan 1965 to Sep 2012. Data source: EIA.
Fuel efficiency of vehicles sold in the United States has been increasing rapidly over the last five years, meaning that the typical new car gets substantially more miles per gallon than older vehicles. If Americans just keep buying cars that are no more efficient than the typical model sold in 2012, average fuel efficiency of the existing fleet will continue to rise over time, as older cars are scrapped and replaced with new models.

Average miles per gallon of passenger vehicles sold in the United States, monthly Oct 2007 to Oct 2012. Source:UMTRI.
To get a quick idea for the likely magnitude of this effect, I assumed that the age of the existing fleet can be described using an exponential distribution, according to which the fraction of cars less than x years old can be calculated from the formula 1 - e-gx where g is a parameter that characterizes the distribution. This distribution would arise, for example, if there were no changes over time and if a constant fraction g of existing cars were scrapped and replaced with a new car each year independent of age. Although one could build much more detailed models that take into account differential scrappage and utilization rates by age, the exponential distribution seems appropriate for the kind of ballpark calculations I'm interested in here. The average age of cars currently being driven has been separately estimated to be around 11 years, which would imply a value of g = 1/11. As a separate check on the plausibility of the assumption of an exponential distribution, the model predicts that a fraction 1 - e-1/11 = 0.087 of the cars currently on the road should be less than 1 year old. In 2010 there were 131 million automobiles registered in the United States and 11.5 million new passenger vehicles sold, for a directly calculated ratio of 11.5/131 = 0.088. So I'm comfortable using the exponential distribution for calculations like the ones I'm about to report.
To use this distribution, I need a longer time series for the fuel efficiency of new vehicles, for which I used figures reported by the NHTSA shown in the graph below. These systematically report miles per gallon to be a higher number than the EPA sticker figures in the graph above. However, all the key calculations below refer to changes over time, so if the official NHTSA figures at least have accurate estimates of the rate of change in mpg of new cars sold from one year to the next, the estimates below will still be accurate.
Related Article: U.S. Energy Department Report Supports Shale Boom Credibility

Blue line: Average miles per gallon of passenger vehicles sold in the United States, annually 1978 to 2012, from NHTSA. Scenario 1 assumes this stays frozen at current value of 33.2 mpg, while Scenario 2 assumes it increases by 2.5% per year.
Given the history of the average mileage of new vehicles sold each year (the blue line in the figure above) and an assumed fraction of cars of each age still on the road implied by the exponential distribution, I calculated the current average fuel economy of the existing fleet to be 27 mpg-- this is essentially just a geometric weighted average of the most recent values for the blue line in the graph above. If new cars offer 33 mpg, the average fuel economy of the existing fleet will continue to rise with time even if nothing else changes. For example, if the fuel efficiency of new cars sold in 2013 is no better than it was in 2012, the average fuel economy of the typical car on the road will improve to 27.6 mpg next year as more 33 mpg cars replace some of the less fuel-efficient models currently on the road. If there are no further improvements in fuel efficiency over the next decade, I calculate that the average car on the road would be getting 30.5 mpg by 2020.
However, current Corporate Average Fuel Economy (CAFE) rules call for increasing mileage standards over this decade. MIT Professor Christopher Knittel estimates that technological progress would allow average miles per gallon to grow by about 2% per year with constant vehicle size and horsepower, and torque, and faster if we gradually move to smaller cars. In Scenario 2 in the graph above, I assume that the average miles per gallon of newly sold vehicles increases by 2.5% per year. That would result in slightly better mileage each year than anticipated to result from current CAFE standards. Under this scenario, the average efficiency for existing cars would rise to 27.7 mpg in 2013 and 32.8 by 2020, when the average new car sold in 2020 is assumed to get 40.5 mpg as measured by the NHTSA (translating into a presumed EPA sticker mileage of perhaps 30 mpg).
The next question is how much a reduction in consumption this would translate into. First suppose that the total number of miles driven never goes up from 2012 levels. That would mean a ratio of gallons consumed in 2013 to gallons consumed in 2012 of (27.0/27.6) = 0.978 or a 2.2% reduction under Scenario 1 and a 2.4% reduction under Scenario 2. By 2020 we would have an 11.4% reduction under Scenario 1 and a 17.8% reduction under Scenario 2.
But does it make any sense to expect that total miles driven remains frozen? Historically, it would usually take both a significant recession and a big spike in oil prices to produce a temporary dip down in U.S. vehicle miles traveled. Nevertheless, so far there is no sign of U.S. miles driven climbing back up to where it had been prior to the Great Recession.
Related Article: Energy Juniors Eye Somaliland Oil Potential

Source: Calculated Risk.
Bill McBride notes that the drop in miles driven since 2007 is not just due to higher gasoline prices and the weak economy. Older people drive less than younger, so as America ages, that would be a factor offsetting the effects of higher income and a growing population and leading us to expect a slower growth rate over the next decade than we have seen previously. Bill also reports evidence of a values shift of younger people away from cars, and some changes in patterns of home and work location that reduce total driving.

Source: Calculated Risk.
ADVERTISEMENT
Miles driven grew at an average annual rate of 2.7% between 1980 and 2005. Suppose for illustration we believed that demographic and values shifts will result in growth at less than half that rate over the next decade. That would mean a net drop in U.S. oil consumption next year of 1.3 - 2.2 = -0.9% under Scenario 1 and a drop by 2020 of (8)(1.3) - 11.4 = -1.0%. By contrast, under Scenario 2 we'd be talking about a 7.4% decline by 2020. With current oil consumption around 18.7 mb/d, that would correspond to a saving of 1.4 mb/d by 2020.
Note these calculations do not take into account further possible reductions from increased use of biofuels and natural gas for transportation.
My conclusion is that if the price of oil remains at its current value, an ongoing decline in U.S. oil consumption over the next decade is a plausible baseline scenario even without the currently planned CAFE standards. If the price rises modestly from its current value (as the IEA analysis assumes), given the increased commitment to conservation already embodied in current standards, a reduction in consumption by 2020 of the size assumed in the IEA report looks reasonable.
By. James Hamilton
Source: Econbrowser